そのMiddle-out approach、大丈夫ですか?(3)
2023-06-11
これまでのブログで、以下のような考察が得られました。
・Middle-out approachを行うのは、Buttom-up予測が外れたから。(外れた結果を隠さないで!!!科学が発展しなくなってしまいます)。
・1つの血中濃度推移データから逆算できるパラメータ数は少ない(せいぜい1-2個まで?)。
・血中濃度推移データからパラメータを逆算した適合PBPKモデルは、その血中濃度推移データを「記述」しているのであり、「予測」しているのではない。
それでは、Bottom-up予測が外れた場合、PBPKの数多くのパラメータの中から、どのパラメータを選んで、逆算すべきなのでしょうか?
(H)できれば、あとから選ばなくてよい状況にしよう!
まずはじめに、この疑問を抱くということは、パラメータの逆算を、あらかじめ視野に入れた試験計画ではなかった、ということですね。もし、はじめから計画していたのでしたら、迷わずに、そのパラメータを選択するでしょう???
実験データから決定できるパラメータは、実験データの組によります。特異的阻害剤併用の有無における血中濃度推移データからは、その阻害剤が阻害するクリアランス経路の寄与率を決定できます。
繰り返しになりますが、逆算したいパラメータに合わせて、そのパラメータを逆算できる試験計画にすべきということです(例えば、Fを求めるには、i.v.とp.o.が必要ですよね)。
しかし、実際には、あらかじめ逆算に用いることを前提とした試験になっていない場合もあるでしょう? その場合、どのパラメータを選びますか?
現在は、ひとにより、それぞれです。各自が、好き勝手に決めています。それって、大丈夫なのでしょうか?そんなことをしたら、各自(各社?)、自分が有利になるようにパラメータを勝手に選んでしまうのではないでしょうか?
残念ながら、現在はそうなっています。
(I)感度分析で何がわかるのか?
逆算するパラメータを選ぶために、感度分析がしばしば利用されます。感度分析を用いれば、客観的にパラメータを選ぶことが出来るのでしょうか?
答えは、Yesであり、Noです。
まず、Yesから説明します。
当たり前ですが、あるパラメータを変化させても計算出力値に影響がない場合(感度が無い場合)、そのパラメータは試験結果から逆算できません。つまり、感度分析では、逆算できないパラメータはどれなのか?がわかります。
(前回のブログで説明した最小二乗法を考えれば、パラメータを変化させても計算出力値が変化しないのであれば、残差も変化しません。残差平方和はパラメータに依存せず一定になり、極小値が無いので最適化できない(逆算できない)ことがわかります。)
一般に、速度論において、出力値に影響を与えるのは、一連の反応プロセスの中で「律速段階」となる反応だけです。したがって、律速段階以外のプロセスのパラメータを試験結果から逆算することは出来ません。
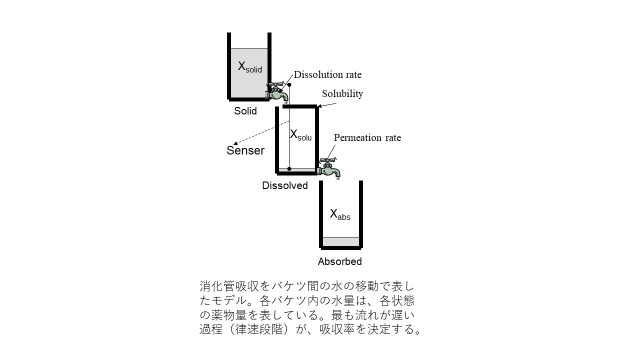
重要なのは、律速段階を把握することであり、感度分析はその1つのツールにすぎません。まずはじめに、律速段階を把握することに注力しましょう。これは、薬物動態に限らず、すべての速度論に共通して、基礎となる、最も重要なことです。律速段階を把握するには、各過程の速度定数を計算して比較すればOKです。感度分析だけに頼るのは、かえってモデルの理解を妨げてしまいます。感度分析は統計的Black boxモデルには有用なのですが、PBPKはメカニズムベースなので、各過程の速度定数を計算できます。
次にNoについてです。
PBPKモデルでは、律速段階が複数のパラメータで表されます。
例えば、肝クリアランスでは
CLh = fup x CLint(肝血流量よりも、十分低い場合)
したがって、感度分析をすれば、fupもCLintも同じようにCLhを変化させます。タンパク結合率と固有肝クリアランスのどちらを逆算すべきか?は感度分析からは解りません。通常は、タンパク結合率はin vitroで正確に測定できると別途に仮定して、CLintを最適化します。しかし、この仮定は正しくないかもしれないです(fup < 0.01では正確に測定するのが難しいので。。。)。実際には、肝以外にもクリアランス経路があるかもしれないですし。。。
まとめると、感度分析では、どのパラメータを逆算できないかはわかりますが、逆算できる可能性のある多数のパラメータから、どれか1つを選ぶことはできません。。
(J)スケーリングファクター?
それでは、パラメータを選ぶのはあきらめて、思い切って、エラー補正ファクター(ECF)を新たに導入し、それを逆算しよう!と考えるかもしれないですね。例えば
CLh = ECF x fup x CLint(肝血流量よりも、十分低い場合)
ここでは、fupとCLintは、in vitroからの予測値そのままになります。
まず、はじめに気を付けないといけないのは、ECFには実体がないということです。したがって、PBPKの本来の方向性に反して、実体のないものをPBPKに持ち込むということです。つまりは、経験モデルが持ち込まれますので、その使用は経験モデルの使用ルールに従うべきです(内挿に限るとか。。。独立したデータ(テストセット)で検証が必要とか。。。)。
また、ECFを逆算することと、他の何かのパラメータを逆算することは、数学的に同じです。
ECF x fup,in vitro = fup,逆算
と、ひとまとめにできますので。。。
ただ、ECFを用いたほうが誤解が少ないでしょう。
ECFは、一部の市販PBPKソフトでは別名スケーリングファクターと呼ばれています。しかし、これは大きな誤解を招く表現なのではないかと思います。スケーリングファクターとは、一般には、相似形の比(スケール)を換算する際に用いる用語です。
さらなる注意点もあります。もちろん、ECFを導入して、それを血中濃度推移から逆算すれば、得られた適合モデルは、元となる血中濃度推移にぴったりと一致します。しかし、このことは、モデルが正しいことを示しているのではありません。さらには、他のパラメータが正しいわけでもありません。たとえば、CLintが10倍低く間違っていても、ECFを10倍すればよいため、エラーはすべてECFに隠されてしまいます。しかし、血中濃度推移にぴったりと一致したシミュレーションを見たら、CLintが正しいと錯覚してしまうのではないでしょうか?実際、この結果からは、in vitroから予測したCLintとfupについて、どちらが、どれだけ、間違っているのかはわかりません。このような状態で、次の別の条件下での結果を予測しても良いのか?疑問ですよね?
これらの注意点がありますが、律速段階の部分のモデル式に、1つだけECFを導入して、それを逆算することは可能でしょう。その方が、複数のパラメータを最適化してしまうリスクは無くなります。
ただ、それならば、いっそのこと、律速段階の速度論的パラメータ(例えば吸収速度定数(ka))を、そのまま丸ごと逆算し、次の予測に用いるということも考えられます。その方が、誤解が少ないです(人類のこれまでの経験から、一般には、不必要に複雑なモデルを用いるのは良くないとされています(オッカムの剃刀)。
それでは、次のブログでは、ある条件下で得られた適合PBPKモデルの、他の条件に対する予測性をどのように検証(validation)していくべきかを議論します。
・Middle-out approachを行うのは、Buttom-up予測が外れたから。(外れた結果を隠さないで!!!科学が発展しなくなってしまいます)。
・1つの血中濃度推移データから逆算できるパラメータ数は少ない(せいぜい1-2個まで?)。
・血中濃度推移データからパラメータを逆算した適合PBPKモデルは、その血中濃度推移データを「記述」しているのであり、「予測」しているのではない。
それでは、Bottom-up予測が外れた場合、PBPKの数多くのパラメータの中から、どのパラメータを選んで、逆算すべきなのでしょうか?
(H)できれば、あとから選ばなくてよい状況にしよう!
まずはじめに、この疑問を抱くということは、パラメータの逆算を、あらかじめ視野に入れた試験計画ではなかった、ということですね。もし、はじめから計画していたのでしたら、迷わずに、そのパラメータを選択するでしょう???
実験データから決定できるパラメータは、実験データの組によります。特異的阻害剤併用の有無における血中濃度推移データからは、その阻害剤が阻害するクリアランス経路の寄与率を決定できます。
繰り返しになりますが、逆算したいパラメータに合わせて、そのパラメータを逆算できる試験計画にすべきということです(例えば、Fを求めるには、i.v.とp.o.が必要ですよね)。
しかし、実際には、あらかじめ逆算に用いることを前提とした試験になっていない場合もあるでしょう? その場合、どのパラメータを選びますか?
現在は、ひとにより、それぞれです。各自が、好き勝手に決めています。それって、大丈夫なのでしょうか?そんなことをしたら、各自(各社?)、自分が有利になるようにパラメータを勝手に選んでしまうのではないでしょうか?
残念ながら、現在はそうなっています。
(I)感度分析で何がわかるのか?
逆算するパラメータを選ぶために、感度分析がしばしば利用されます。感度分析を用いれば、客観的にパラメータを選ぶことが出来るのでしょうか?
答えは、Yesであり、Noです。
まず、Yesから説明します。
当たり前ですが、あるパラメータを変化させても計算出力値に影響がない場合(感度が無い場合)、そのパラメータは試験結果から逆算できません。つまり、感度分析では、逆算できないパラメータはどれなのか?がわかります。
(前回のブログで説明した最小二乗法を考えれば、パラメータを変化させても計算出力値が変化しないのであれば、残差も変化しません。残差平方和はパラメータに依存せず一定になり、極小値が無いので最適化できない(逆算できない)ことがわかります。)
一般に、速度論において、出力値に影響を与えるのは、一連の反応プロセスの中で「律速段階」となる反応だけです。したがって、律速段階以外のプロセスのパラメータを試験結果から逆算することは出来ません。

重要なのは、律速段階を把握することであり、感度分析はその1つのツールにすぎません。まずはじめに、律速段階を把握することに注力しましょう。これは、薬物動態に限らず、すべての速度論に共通して、基礎となる、最も重要なことです。律速段階を把握するには、各過程の速度定数を計算して比較すればOKです。感度分析だけに頼るのは、かえってモデルの理解を妨げてしまいます。感度分析は統計的Black boxモデルには有用なのですが、PBPKはメカニズムベースなので、各過程の速度定数を計算できます。
次にNoについてです。
PBPKモデルでは、律速段階が複数のパラメータで表されます。
例えば、肝クリアランスでは
CLh = fup x CLint(肝血流量よりも、十分低い場合)
したがって、感度分析をすれば、fupもCLintも同じようにCLhを変化させます。タンパク結合率と固有肝クリアランスのどちらを逆算すべきか?は感度分析からは解りません。通常は、タンパク結合率はin vitroで正確に測定できると別途に仮定して、CLintを最適化します。しかし、この仮定は正しくないかもしれないです(fup < 0.01では正確に測定するのが難しいので。。。)。実際には、肝以外にもクリアランス経路があるかもしれないですし。。。
まとめると、感度分析では、どのパラメータを逆算できないかはわかりますが、逆算できる可能性のある多数のパラメータから、どれか1つを選ぶことはできません。。
(J)スケーリングファクター?
それでは、パラメータを選ぶのはあきらめて、思い切って、エラー補正ファクター(ECF)を新たに導入し、それを逆算しよう!と考えるかもしれないですね。例えば
CLh = ECF x fup x CLint(肝血流量よりも、十分低い場合)
ここでは、fupとCLintは、in vitroからの予測値そのままになります。
まず、はじめに気を付けないといけないのは、ECFには実体がないということです。したがって、PBPKの本来の方向性に反して、実体のないものをPBPKに持ち込むということです。つまりは、経験モデルが持ち込まれますので、その使用は経験モデルの使用ルールに従うべきです(内挿に限るとか。。。独立したデータ(テストセット)で検証が必要とか。。。)。
また、ECFを逆算することと、他の何かのパラメータを逆算することは、数学的に同じです。
ECF x fup,in vitro = fup,逆算
と、ひとまとめにできますので。。。
ただ、ECFを用いたほうが誤解が少ないでしょう。
ECFは、一部の市販PBPKソフトでは別名スケーリングファクターと呼ばれています。しかし、これは大きな誤解を招く表現なのではないかと思います。スケーリングファクターとは、一般には、相似形の比(スケール)を換算する際に用いる用語です。
さらなる注意点もあります。もちろん、ECFを導入して、それを血中濃度推移から逆算すれば、得られた適合モデルは、元となる血中濃度推移にぴったりと一致します。しかし、このことは、モデルが正しいことを示しているのではありません。さらには、他のパラメータが正しいわけでもありません。たとえば、CLintが10倍低く間違っていても、ECFを10倍すればよいため、エラーはすべてECFに隠されてしまいます。しかし、血中濃度推移にぴったりと一致したシミュレーションを見たら、CLintが正しいと錯覚してしまうのではないでしょうか?実際、この結果からは、in vitroから予測したCLintとfupについて、どちらが、どれだけ、間違っているのかはわかりません。このような状態で、次の別の条件下での結果を予測しても良いのか?疑問ですよね?
これらの注意点がありますが、律速段階の部分のモデル式に、1つだけECFを導入して、それを逆算することは可能でしょう。その方が、複数のパラメータを最適化してしまうリスクは無くなります。
ただ、それならば、いっそのこと、律速段階の速度論的パラメータ(例えば吸収速度定数(ka))を、そのまま丸ごと逆算し、次の予測に用いるということも考えられます。その方が、誤解が少ないです(人類のこれまでの経験から、一般には、不必要に複雑なモデルを用いるのは良くないとされています(オッカムの剃刀)。
それでは、次のブログでは、ある条件下で得られた適合PBPKモデルの、他の条件に対する予測性をどのように検証(validation)していくべきかを議論します。

