そのMiddle-out approach、大丈夫ですか?(2)
2023-06-11
前回のブログで、血中濃度推移から何個のパラメータを決定できるか?お話ししました。
横軸を時間、縦軸を血中濃度(Cp)の対数(lnCp)としてプロットしたとき、直線っぽくなる部分の数が1つなら2個のパラメータ、2つなら4個のパラメータまでです。それ以上のパラメータを決定することは、過剰適合になってしまうので、出来ないのでした。
それでは、パラメータ数が非常に多数あるPBPKモデルにおいて、血中濃度推移からパラメータ値を逆算できるでしょうか?もちろん、PBPKモデルのすべてのパラメータを、血中濃度推移から決定することはできません。したがって、middle-outでは、多数あるパラメータの中から、少数を選んで逆算することになります。
ここからは、PBPKモデルにおけるmiddle-out approachについて考えていきますが、まずはじめに、どうしてmiddle-outが提唱されてきたのか?考えてみたいと思います。
(D)なぜmiddle out approachが必要なのか?
PBPKモデルは、そもそも、生理学的パラメータと、物性データやin vitroデータから、血中濃度推移を”予測”することを目指しています(これをBottom-up予測と言います)。PBPKは、そもそもコンパートメントモデルとは全く方針が違うのです(コンパートメントモデルは、もしろ、物理的実体を反映していない(統計的な)経験モデルの仲間と言えるでしょう。)。
したがって、血中濃度推移からのパラメータ逆算、すなわち、middle-out approachは、本来のPBPKの方向性とは異なります。まず、このことは、しっかりと認識しておきましょう。(僕が頭が固い!のかもしれないですが。。。)
それでは、なぜ、多くの論文で、血中濃度推移からのパラメータ逆算(top-down)が、PBPKに取り入れられているのでしょうか?
(Bottom-upとtop-downを混ぜているので、middle-outと呼ぶようです。)
理由は、現在の我々の知識では、bottom-upでは、血中濃度推移を十分な精度で予測することが出来ないからです。(ここでは、「十分な精度」は、実測値の0.8-1.25倍程度をイメージしてください。)
現在、bottom-upによる予測精度は、静脈内投与後の血中濃度推移で3倍程度以上の誤差があり、経口吸収率(Fa)についても2倍程度の誤差があります(フリー体原薬の場合)。このことも、しっかりと認識しておきましょう。
大変残念ながら、多くのPBPK論文では、bottom-upによる外れた予測結果は隠蔽されています。これは科学論文として、決して良いことではありません。
(PBPKの論文を書かれる方は、bottom-up予測が外れた結果も、必ず載せてください。予測が外れることは、恥ずかしいことではありません。むしろ、科学の発展につながる大切なことです。しかし、外れた予測を隠蔽するのは、科学者として恥ずかしいことです。)
Bottom-upでは予測精度が足りない。現在のPBPKは、まだまだ不十分だ。では、どうするか?
もちろん、正攻法は、in vitro試験法、生理学的パラメータ、数理モデルの研究を発展させることです。これを忘れてはいけません。忘れてしまうと、薬物動態研究は、終わってしまいます。薬物動態には、まだまだ研究すべきことがたくさんあります。
でも、現実問題として、何とか今すぐに、血中濃度推移を精度よく予測したい。例えば、FIH試験(健常人、単回)における血中濃度推移データをPBPKに活用して、他の条件下における予測精度を向上できるのではないか?そこで、middle-outという考え方が、出てきました。(なお、PBPK以外の予測方法もあります。PBPKがすべてではないです。)
ここで、赤色を付けた単語に注意してください。FIHの血中濃度推移データを記述できるか?ではありません。他の条件下の予測です。
(E) 何個のパラメータを血中濃度推移から決定できるのか?
静脈内投与の血中濃度推移からは、何個までパラメータを決定できるのでしょうか?これまでの議論を思い出すと、せいぜい2から4個程度だろうと考えられます。
経口吸収モデルのパラメータを逆算するには、さらに経口投与後の血中濃度推移が必要になります。これまでの議論を思い出すと、これで逆算できるパラメータ数は、たったの1つだったのでしたね?
このように、血中濃度推移から決定できるパラメータ数には、数学的な制限があります(”次元の呪い”)。したがって、これ以上の数のパラメータを逆算(パラメータフィッテイング)している論文は、信用できません。
コンパートメントモデルの例を見ればわかる通り、ほんの少数のパラメータだけを持つ数理モデルでも、血中濃度推移に適合するようにパラメータを逆算すれば、ほぼ完ぺきに血中濃度推移を「記述」できます。同様に、PBPKモデルでも、少数のパラメータを逆算すれば、ほぼ完ぺきに血中濃度推移を「記述」できます。しかし、前回のブログでも議論したように、この完璧に見える「記述」は、PBPKモデルが正しいことを示しているわけではありませんし、予測性が良いことを示しているのでもありません。「予測」と「(フィッティングによる)記述」は全く違います。これらを取り違えて、市販PBPKソフトウェアを信じてしまう人たちが後を絶ちません。とくに、経験が浅く、ウェットの実験をしたことがない方、是非ご注意ください。
(F)どうやってパラメータを決定するのか?
では、PBPKモデルのようにパラメータが多数あるモデルにおいて、ある1つのパラメータを決定するにはどうすれば良いのでしょうか?(多数あるパラメータの中から、どのパラメータを選ぶかについては、後ほど議論します。)
ここでは、前回のブログで扱った数式をもう一回考えてみましょう。
w = ax + by + cz + d
というモデル式があるとします。a,b,c,dの四つのパラメータをすべて観察結果から決定しようとすれば、最低限4組のデータポイントが必要です。
しかし、aだけを決定するのであれば、実は2つのデータポイントだけで済みます。
どうやって???
まず、ある組の条件(x1,y1,z1)で、1回実験をします。ここで得られた結果をw1とします。
w1 = ax1 + by1 + cz1 + d
次に、xを0に設定し(x = 0となるように「介入」し)、他の条件はそのままでもう一回実験します。ここで得られた結果をw2とします。
w2 = by1 + cz1 + d
上の式から下の式を引くと
w1-w2 = ax1
です。したがって、
a = x1/(w1-w2)
となってaを求めることが出来ました。この方法は、モデルのパラメータ数がいくつに増えても適応できることは、すぐに解りますね?ax以外の項は、引き算ですべて消えてしまいますよね?
(これは、大学生が研究室で研究を始める際に、一番初めに習うことと基本的に同じです。実験で、ある要因の効果を調べたい場合、その要因以外の条件はすべて同じにしなさい、と先生から習ったと思います。そうすれば2つのデータを比較することで(=引き算することで)、答えが出ます。実験条件を2つ以上同時に変えてはダメですよね。)
ここで大切なのは、x = 0となる条件で試験を行うことです。例えば、ある代謝酵素について、特異的かつ強力な阻害剤を同時投与した場合が、これにあたります。
CLが、いくつかの経路の足し算、
CL実測 = CL1 + CL2 + CL3 +++++
で表せる場合、CL1に対する阻害剤が無い場合とある場合の実測データがあれば、
CL1 = CL実測阻害剤あり-CL実測阻害剤なし
となって、CL1を計算できるのでした。この結果を基にして、”別の”薬物を同時投与した際のCLを”予測値”を計算できることになります。(予測値を計算できることと、その予測の精度が良いか?は別問題です。例えば、天気の予測値を出すこと自体は、下駄投げでもできます。しかし、それでは当たりませんよね。予測”できる”という単語に2重の意味が入っていることもありますので注意しましょう。)。
ここで、一つ重要なことがあります。それは、この方法は、複雑なPBPKモデルでなくても良いということです。実際、mechanistic static modelでも、同様に、薬物相互作用を予測できます。予測精度も、動的なPBPKと同程度であることが知られています(FDAへの申請書を解析した結果の論文があります)。それでは、複雑なPBPKと簡単なmechanistic static modelのどちらが良いのでしょうか?これについては、また別の機会に議論します。
------
ここでは、簡単なmechanistic static modelでも、PBPKと同程度の精度で予測できると言うことだけ述べておきます。Mechanistic static modelは、多数の組み合わせのDDIで”予測”性が系統的に検証されています。したがって、エビデンスレベルが高いです。PBPKによる”予測”のエビデンスレベルは???ソフトウェアメーカーの宣伝を鵜呑みにしないで、是非、各自で調査し、考えてみてください。)
----
(発展版)
実は、この方法は、x = 0でなくて、x = 0.5の場合でも使用できます。また、特異性が低く、複数の酵素を阻害する場合でも、その分、いろいろな薬物と併用時の血中濃度推移を複数組み合わせて同時に解析すれば、パラメータを逆算できます(計算はややこしくなりますが)。その他、代謝物プロファイルと組み合わせるなど、様々な解析方法も考えられます。ただ、いずれにせよ、実験データの数は、逆算するパラメータ数より多い必要があります。次元の呪いを乗り越えることは出来ません。また、データの数が増えれば、その分、不確実性も増えます(in silicoだけをやっている人にはわからないかもしれないですが、実験データとはそういうものです。)。したがって、あるパラメータを確実に逆算するには、可能な限り、強力かつ特異的にx = 0となるような方法を選びます。つまり、パラメータを決められるように、あらかじめ試験計画を立てることが肝心です。医薬品開発では、臨床試験計画を自ら立てられるのですから、確実にパラメータを逆算できる試験計画を立てましょう。逆説的になりますが、そのためにBottom-upのPBPK予測を使うのは、とても有用だと思います。
---
(G)パラメータ最適化とはなにか?
これまでの説明では、非常に簡単な数理モデルを用いていました。これらの場合、足し算引き算程度で、実測データからパラメータを逆算できました。
それでは、より複雑なモデル、特に、非線形と呼ばれるモデルでは、どのようにしてパラメータを血中濃度推移から逆算するのでしょうか?
一般に用いられるのは、最小二乗法と呼ばれる方法です。最小二乗法では、数理モデルにより記述される曲線と実験データポイントの間の「距離」が「最も短く」なるようなパラメータ値を逆算します。
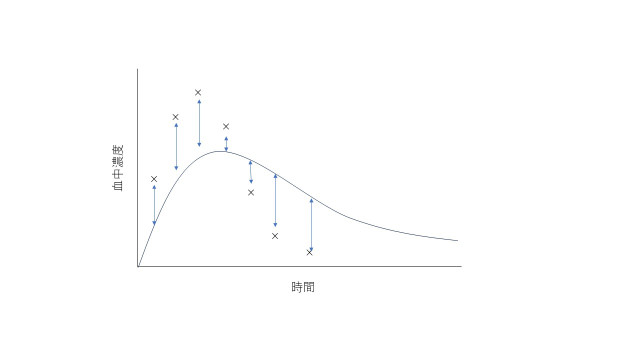
データとデータの距離とは何でしょうか?
ある1つのデータポイントについて、実験値と、モデルによる計算値との間の距離(残差)は
s = (実験-計算)^2
として表せます。ここで2乗するのは、距離がマイナスになってしまうのを防ぐためです。これを残差平方と言います。
すべてのデータポイントについて、残差平方を足し合わせたものは、残差平方和あるいは二乗和(sum of square)と呼ばれます。
ss = すべてのデータポイントの残差平方を合計した値
そして、残差平方和(ss)が最少になるパラメータの値を探すことで、実測データに最もよく適合した数理モデルを作成できます。
これが、最小二乗法と呼ばれる方法です。
(ssは2乗和なので、必ず、0以上で最小になる値があります)。
それでは、どうやってssが最小になるパラメータ値を探すのでしょうか?
これには、いくつかの方法があります。
代表的な方法は、ニュートン法と呼ばれています。
ニュートン法を理解するために、曲線の上を歩くアリさんになったと想像してみましょう。
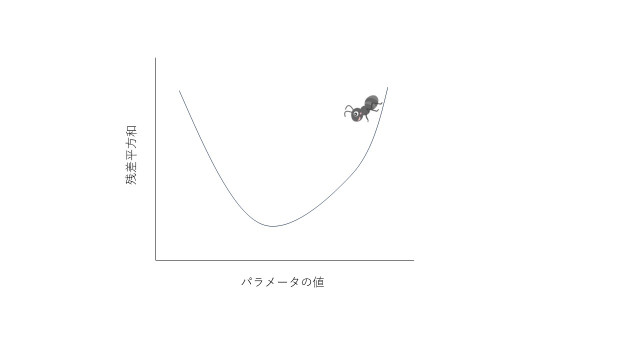
この図で、横軸は求めたいパラメータ、縦軸は最小二乗法です。
アリさんには、谷底まで行ってね、と伝えておきます。すると、アリさんは坂が下っている方向に歩いていきます(アリさんは、足元の傾斜はわかるので)。しばらくすると、今度は、上り坂になりますので、その直前でとまります。これで、無事に谷底に到達しました。めでたし、めでたし。
このように、ある元のパラメータ値(初期値)から出発して、坂が下る方向へ向かい、残差平方和が最少になる場所を探す方法をニュートン法と言います。上り下りの方向は、傾きから計算します。ニュートン法では初期値からパラメータ値をずらしながら谷底を探すので、「最適化(optimize)」や「調整(adjust)」などと呼ばれています。しかし、これらの言葉が与えるニュアンスとは異なり、実際には、元の値とは全く違う値になる場合も多いです。なお、この機能は、エクセルではsolverと呼ばれています。
この図の場合、初期値は図中のどこから出発しても良いです。PBPKでは、初期値としてin vitroからの予測値を用いている場合が多いと思います。しかし、in vitroからの予測値を微調整しているわけではありません。単に出発点してとりあえず使っているだけで、最適化後の値は、基本的に初期値とは無関係です。勘違いしないようにしましょう。
自分は、ニュアンスが間違って伝わらないように、逆算(back calculation)と呼ぶようにしています。例えば、前回のブログにおける、連立方程式を解く場合を思い出してみてください。パラメータの逆算に、初期値は必要ありませんよね?先ほどの阻害剤存在下データからのCL1の計算も同様に、初期値は必要ありません。
(ベイズ統計を用いれば、in vitroからのパラメータ予測値をin vivoのデータで更新することもできます。しかし、ニュートン法では元のデータは関係ありません。初期値は、あてずっぽうでも構わないと言えば構わないのです(収束するかは別にして))。
ちなみに、アリさんのように徐々に探していくことも可能ですが、ほかにも、キリギリスさんのように、ピョンピョン飛びながら探すことも可能です(simplex法のイメージ)。
今度は、次の図のように、谷底が幾つかある場合を考えてみましょう。
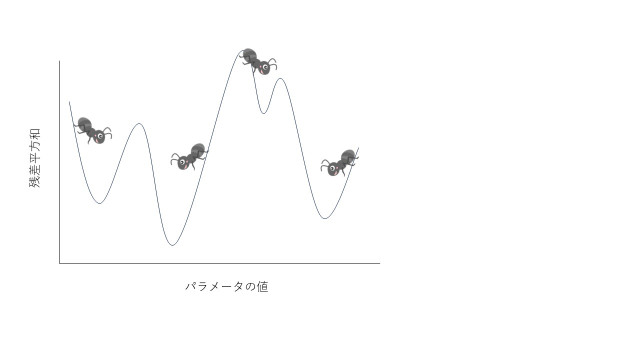
先ほどと同様にアリさんには谷底まで歩いてもらいます。この時、それぞれのアリさんで、たどり着く谷底が違います。我々が求めたいのは、残差平方和が最小になるパラメータ値ですので、例えば、左端から歩くアリさんは困ってしまいます(このアリさんがたどり着いた解を、局所解と言います)。
解決策の一つとしては、様々な初期値から探索を繰り返して、一番低い場合を選択するという方法が考えられます。
このように工夫すれば、局所解にトラップされてしまうという問題はある程度回避できます。しかし、これで、”次元の呪い”を回避できるわけではありません。あくまで、局所解にならないための工夫です。誤解されないように。。。
このようにして、パラメータを1-2個選び、血中濃度に適合(フィッティング)するように逆算すれば、血中濃度を記述できるPBPKモデル(適合モデル)が完成します。(繰り返しになりますが、”予測”ではありません。)
それでは、PBPKモデルの中の、どのパラメータを選んで、逆算すべきなのでしょうか?そして、ある条件下における既知データに対して得られた適合PBPKモデルについて、他の条件に対する”予測”性は、どのように検証すれば良いのでしょうか?これについては、次回のブログで考えていきたいと思います。
横軸を時間、縦軸を血中濃度(Cp)の対数(lnCp)としてプロットしたとき、直線っぽくなる部分の数が1つなら2個のパラメータ、2つなら4個のパラメータまでです。それ以上のパラメータを決定することは、過剰適合になってしまうので、出来ないのでした。
それでは、パラメータ数が非常に多数あるPBPKモデルにおいて、血中濃度推移からパラメータ値を逆算できるでしょうか?もちろん、PBPKモデルのすべてのパラメータを、血中濃度推移から決定することはできません。したがって、middle-outでは、多数あるパラメータの中から、少数を選んで逆算することになります。
ここからは、PBPKモデルにおけるmiddle-out approachについて考えていきますが、まずはじめに、どうしてmiddle-outが提唱されてきたのか?考えてみたいと思います。
(D)なぜmiddle out approachが必要なのか?
PBPKモデルは、そもそも、生理学的パラメータと、物性データやin vitroデータから、血中濃度推移を”予測”することを目指しています(これをBottom-up予測と言います)。PBPKは、そもそもコンパートメントモデルとは全く方針が違うのです(コンパートメントモデルは、もしろ、物理的実体を反映していない(統計的な)経験モデルの仲間と言えるでしょう。)。
したがって、血中濃度推移からのパラメータ逆算、すなわち、middle-out approachは、本来のPBPKの方向性とは異なります。まず、このことは、しっかりと認識しておきましょう。(僕が頭が固い!のかもしれないですが。。。)
それでは、なぜ、多くの論文で、血中濃度推移からのパラメータ逆算(top-down)が、PBPKに取り入れられているのでしょうか?
(Bottom-upとtop-downを混ぜているので、middle-outと呼ぶようです。)
理由は、現在の我々の知識では、bottom-upでは、血中濃度推移を十分な精度で予測することが出来ないからです。(ここでは、「十分な精度」は、実測値の0.8-1.25倍程度をイメージしてください。)
現在、bottom-upによる予測精度は、静脈内投与後の血中濃度推移で3倍程度以上の誤差があり、経口吸収率(Fa)についても2倍程度の誤差があります(フリー体原薬の場合)。このことも、しっかりと認識しておきましょう。
大変残念ながら、多くのPBPK論文では、bottom-upによる外れた予測結果は隠蔽されています。これは科学論文として、決して良いことではありません。
(PBPKの論文を書かれる方は、bottom-up予測が外れた結果も、必ず載せてください。予測が外れることは、恥ずかしいことではありません。むしろ、科学の発展につながる大切なことです。しかし、外れた予測を隠蔽するのは、科学者として恥ずかしいことです。)
Bottom-upでは予測精度が足りない。現在のPBPKは、まだまだ不十分だ。では、どうするか?
もちろん、正攻法は、in vitro試験法、生理学的パラメータ、数理モデルの研究を発展させることです。これを忘れてはいけません。忘れてしまうと、薬物動態研究は、終わってしまいます。薬物動態には、まだまだ研究すべきことがたくさんあります。
でも、現実問題として、何とか今すぐに、血中濃度推移を精度よく予測したい。例えば、FIH試験(健常人、単回)における血中濃度推移データをPBPKに活用して、他の条件下における予測精度を向上できるのではないか?そこで、middle-outという考え方が、出てきました。(なお、PBPK以外の予測方法もあります。PBPKがすべてではないです。)
ここで、赤色を付けた単語に注意してください。FIHの血中濃度推移データを記述できるか?ではありません。他の条件下の予測です。
(E) 何個のパラメータを血中濃度推移から決定できるのか?
静脈内投与の血中濃度推移からは、何個までパラメータを決定できるのでしょうか?これまでの議論を思い出すと、せいぜい2から4個程度だろうと考えられます。
経口吸収モデルのパラメータを逆算するには、さらに経口投与後の血中濃度推移が必要になります。これまでの議論を思い出すと、これで逆算できるパラメータ数は、たったの1つだったのでしたね?
このように、血中濃度推移から決定できるパラメータ数には、数学的な制限があります(”次元の呪い”)。したがって、これ以上の数のパラメータを逆算(パラメータフィッテイング)している論文は、信用できません。
コンパートメントモデルの例を見ればわかる通り、ほんの少数のパラメータだけを持つ数理モデルでも、血中濃度推移に適合するようにパラメータを逆算すれば、ほぼ完ぺきに血中濃度推移を「記述」できます。同様に、PBPKモデルでも、少数のパラメータを逆算すれば、ほぼ完ぺきに血中濃度推移を「記述」できます。しかし、前回のブログでも議論したように、この完璧に見える「記述」は、PBPKモデルが正しいことを示しているわけではありませんし、予測性が良いことを示しているのでもありません。「予測」と「(フィッティングによる)記述」は全く違います。これらを取り違えて、市販PBPKソフトウェアを信じてしまう人たちが後を絶ちません。とくに、経験が浅く、ウェットの実験をしたことがない方、是非ご注意ください。
(F)どうやってパラメータを決定するのか?
では、PBPKモデルのようにパラメータが多数あるモデルにおいて、ある1つのパラメータを決定するにはどうすれば良いのでしょうか?(多数あるパラメータの中から、どのパラメータを選ぶかについては、後ほど議論します。)
ここでは、前回のブログで扱った数式をもう一回考えてみましょう。
w = ax + by + cz + d
というモデル式があるとします。a,b,c,dの四つのパラメータをすべて観察結果から決定しようとすれば、最低限4組のデータポイントが必要です。
しかし、aだけを決定するのであれば、実は2つのデータポイントだけで済みます。
どうやって???
まず、ある組の条件(x1,y1,z1)で、1回実験をします。ここで得られた結果をw1とします。
w1 = ax1 + by1 + cz1 + d
次に、xを0に設定し(x = 0となるように「介入」し)、他の条件はそのままでもう一回実験します。ここで得られた結果をw2とします。
w2 = by1 + cz1 + d
上の式から下の式を引くと
w1-w2 = ax1
です。したがって、
a = x1/(w1-w2)
となってaを求めることが出来ました。この方法は、モデルのパラメータ数がいくつに増えても適応できることは、すぐに解りますね?ax以外の項は、引き算ですべて消えてしまいますよね?
(これは、大学生が研究室で研究を始める際に、一番初めに習うことと基本的に同じです。実験で、ある要因の効果を調べたい場合、その要因以外の条件はすべて同じにしなさい、と先生から習ったと思います。そうすれば2つのデータを比較することで(=引き算することで)、答えが出ます。実験条件を2つ以上同時に変えてはダメですよね。)
ここで大切なのは、x = 0となる条件で試験を行うことです。例えば、ある代謝酵素について、特異的かつ強力な阻害剤を同時投与した場合が、これにあたります。
CLが、いくつかの経路の足し算、
CL実測 = CL1 + CL2 + CL3 +++++
で表せる場合、CL1に対する阻害剤が無い場合とある場合の実測データがあれば、
CL1 = CL実測阻害剤あり-CL実測阻害剤なし
となって、CL1を計算できるのでした。この結果を基にして、”別の”薬物を同時投与した際のCLを”予測値”を計算できることになります。(予測値を計算できることと、その予測の精度が良いか?は別問題です。例えば、天気の予測値を出すこと自体は、下駄投げでもできます。しかし、それでは当たりませんよね。予測”できる”という単語に2重の意味が入っていることもありますので注意しましょう。)。
ここで、一つ重要なことがあります。それは、この方法は、複雑なPBPKモデルでなくても良いということです。実際、mechanistic static modelでも、同様に、薬物相互作用を予測できます。予測精度も、動的なPBPKと同程度であることが知られています(FDAへの申請書を解析した結果の論文があります)。それでは、複雑なPBPKと簡単なmechanistic static modelのどちらが良いのでしょうか?これについては、また別の機会に議論します。
------
ここでは、簡単なmechanistic static modelでも、PBPKと同程度の精度で予測できると言うことだけ述べておきます。Mechanistic static modelは、多数の組み合わせのDDIで”予測”性が系統的に検証されています。したがって、エビデンスレベルが高いです。PBPKによる”予測”のエビデンスレベルは???ソフトウェアメーカーの宣伝を鵜呑みにしないで、是非、各自で調査し、考えてみてください。)
----
(発展版)
実は、この方法は、x = 0でなくて、x = 0.5の場合でも使用できます。また、特異性が低く、複数の酵素を阻害する場合でも、その分、いろいろな薬物と併用時の血中濃度推移を複数組み合わせて同時に解析すれば、パラメータを逆算できます(計算はややこしくなりますが)。その他、代謝物プロファイルと組み合わせるなど、様々な解析方法も考えられます。ただ、いずれにせよ、実験データの数は、逆算するパラメータ数より多い必要があります。次元の呪いを乗り越えることは出来ません。また、データの数が増えれば、その分、不確実性も増えます(in silicoだけをやっている人にはわからないかもしれないですが、実験データとはそういうものです。)。したがって、あるパラメータを確実に逆算するには、可能な限り、強力かつ特異的にx = 0となるような方法を選びます。つまり、パラメータを決められるように、あらかじめ試験計画を立てることが肝心です。医薬品開発では、臨床試験計画を自ら立てられるのですから、確実にパラメータを逆算できる試験計画を立てましょう。逆説的になりますが、そのためにBottom-upのPBPK予測を使うのは、とても有用だと思います。
---
(G)パラメータ最適化とはなにか?
これまでの説明では、非常に簡単な数理モデルを用いていました。これらの場合、足し算引き算程度で、実測データからパラメータを逆算できました。
それでは、より複雑なモデル、特に、非線形と呼ばれるモデルでは、どのようにしてパラメータを血中濃度推移から逆算するのでしょうか?
一般に用いられるのは、最小二乗法と呼ばれる方法です。最小二乗法では、数理モデルにより記述される曲線と実験データポイントの間の「距離」が「最も短く」なるようなパラメータ値を逆算します。

データとデータの距離とは何でしょうか?
ある1つのデータポイントについて、実験値と、モデルによる計算値との間の距離(残差)は
s = (実験-計算)^2
として表せます。ここで2乗するのは、距離がマイナスになってしまうのを防ぐためです。これを残差平方と言います。
すべてのデータポイントについて、残差平方を足し合わせたものは、残差平方和あるいは二乗和(sum of square)と呼ばれます。
ss = すべてのデータポイントの残差平方を合計した値
そして、残差平方和(ss)が最少になるパラメータの値を探すことで、実測データに最もよく適合した数理モデルを作成できます。
これが、最小二乗法と呼ばれる方法です。
(ssは2乗和なので、必ず、0以上で最小になる値があります)。
それでは、どうやってssが最小になるパラメータ値を探すのでしょうか?
これには、いくつかの方法があります。
代表的な方法は、ニュートン法と呼ばれています。
ニュートン法を理解するために、曲線の上を歩くアリさんになったと想像してみましょう。

この図で、横軸は求めたいパラメータ、縦軸は最小二乗法です。
アリさんには、谷底まで行ってね、と伝えておきます。すると、アリさんは坂が下っている方向に歩いていきます(アリさんは、足元の傾斜はわかるので)。しばらくすると、今度は、上り坂になりますので、その直前でとまります。これで、無事に谷底に到達しました。めでたし、めでたし。
このように、ある元のパラメータ値(初期値)から出発して、坂が下る方向へ向かい、残差平方和が最少になる場所を探す方法をニュートン法と言います。上り下りの方向は、傾きから計算します。ニュートン法では初期値からパラメータ値をずらしながら谷底を探すので、「最適化(optimize)」や「調整(adjust)」などと呼ばれています。しかし、これらの言葉が与えるニュアンスとは異なり、実際には、元の値とは全く違う値になる場合も多いです。なお、この機能は、エクセルではsolverと呼ばれています。
この図の場合、初期値は図中のどこから出発しても良いです。PBPKでは、初期値としてin vitroからの予測値を用いている場合が多いと思います。しかし、in vitroからの予測値を微調整しているわけではありません。単に出発点してとりあえず使っているだけで、最適化後の値は、基本的に初期値とは無関係です。勘違いしないようにしましょう。
自分は、ニュアンスが間違って伝わらないように、逆算(back calculation)と呼ぶようにしています。例えば、前回のブログにおける、連立方程式を解く場合を思い出してみてください。パラメータの逆算に、初期値は必要ありませんよね?先ほどの阻害剤存在下データからのCL1の計算も同様に、初期値は必要ありません。
(ベイズ統計を用いれば、in vitroからのパラメータ予測値をin vivoのデータで更新することもできます。しかし、ニュートン法では元のデータは関係ありません。初期値は、あてずっぽうでも構わないと言えば構わないのです(収束するかは別にして))。
ちなみに、アリさんのように徐々に探していくことも可能ですが、ほかにも、キリギリスさんのように、ピョンピョン飛びながら探すことも可能です(simplex法のイメージ)。
今度は、次の図のように、谷底が幾つかある場合を考えてみましょう。

先ほどと同様にアリさんには谷底まで歩いてもらいます。この時、それぞれのアリさんで、たどり着く谷底が違います。我々が求めたいのは、残差平方和が最小になるパラメータ値ですので、例えば、左端から歩くアリさんは困ってしまいます(このアリさんがたどり着いた解を、局所解と言います)。
解決策の一つとしては、様々な初期値から探索を繰り返して、一番低い場合を選択するという方法が考えられます。
このように工夫すれば、局所解にトラップされてしまうという問題はある程度回避できます。しかし、これで、”次元の呪い”を回避できるわけではありません。あくまで、局所解にならないための工夫です。誤解されないように。。。
このようにして、パラメータを1-2個選び、血中濃度に適合(フィッティング)するように逆算すれば、血中濃度を記述できるPBPKモデル(適合モデル)が完成します。(繰り返しになりますが、”予測”ではありません。)
それでは、PBPKモデルの中の、どのパラメータを選んで、逆算すべきなのでしょうか?そして、ある条件下における既知データに対して得られた適合PBPKモデルについて、他の条件に対する”予測”性は、どのように検証すれば良いのでしょうか?これについては、次回のブログで考えていきたいと思います。

