そのMiddle-out approach、大丈夫ですか?(1)
2023-06-10
現在、生理学的薬物動態モデル(Physiologically-based pharmacokinetic model, PBPK)の論文が、多数報告されています。市販プログラムを用いた研究が多いのですが、そのほとんどすべてにおいて、薬物ごとに、臨床試験の結果に合うようにモデルのパラメータを再計算した、いわゆる「Middle-out approach」が行われています。しかし、私には、ほとんどすべてのMiddle-out approachは、不適切に実施されれているように思われます。「Middle-out approachは、絶対にダメだ!」と言わないのは、ほんのわずかではありますが、正しく実施されている例もあるためです(全体の1%以下かなぁ~?)。そこで、Middle-out approachを適切に行うにはどうしたらよいのか?考えてみたいと思います。
非常に複雑なPBPKモデルについてMiddle-out approachを考えるのは難しいので、簡単なモデル式を使って考えていきたいと思います。
(A)まずは、中学校数学の復習から。。。
中学校の時に、連立1次方程式について習いましたよね?
y = ax + b
という方程式のaとbを求めるにはどうすればよいか?という問題です。
ここでは、この式を、xという条件で実験をすると、yという値が得られる、という数理モデルとして考えます。
この場合、aとbを求めるには、xとyの組が、2つ必要です。
例えば
x = 1, y = 3
x = 2, y = 5
という実験データが得られた場合、
3 = a + b
5 = 2a + b
なので、上の式から、下の式を引いて、
-2 = -a
つまり
a = 2
です。これを上の式に代入すると、
3 = 2 + b
なのでb = 1。
しかがって、
y = 2x + 1
という式が得られました。
実際に、データを入れて試してみると
x = 1の時、y = 2x1 + 1 = 3
x = 2の時、y = 2x2 + 1 = 5
になりました。めでたし、めでたし。。。
(後述しますが、このことからわかるのは、実験結果に合うようにパラメータを逆算した場合(調整、最適化などとも言われますが)、逆算(=モデル構築)に用いた実験条件とその結果の関係をドンピシャで記述できるということです。このことと、異なる実験条件xから未知の実験結果yを「予測」できるかは、まったく別問題です。当たり前のことに思われるかもしれませんが、実際にはかなり混同されています。)
では、もし実験データが1組しかなかったら、どうなるでしょう?
モデル式y = ax + bに対して、実験データが
x = 1, y = 3
だけの場合を考えると、
3 = a + b
になります。
この数式を満たすaとbの組み合わせは、無限にあります。(a, b)= (0, 3), (1,2), (-1, 4)などなど
したがって、データが1組では、aとbを同定することはできません。(Un-identifiable)
同様に、
z = ax + by +c
の場合には、a,b,cを決めるには3つ以上の実験データの組が必要であり、
w = ax + by + cz + d
の場合には、a,b,c,dを決めるには4つ以上の実験データの組が必要です。
つまり、最低限パラメータ数だけ、実験データの組が必要です。
これは、どんなに高度なスーパーコンピュータを使っても、どんなアルゴリズムを使っても、絶対に回避することはできません。
(B) 検量線の話
さてところで、実際の研究では、
y = ax + b (1)
のaとbを、たった2組の(x,y)のデータポイントだけで決定することはありません。
例えば、検量線を作成する場合、少なくとも4-5点のデータポイントを採るでしょう。
ここで、仮に6つの実験データがある場合(図1)、
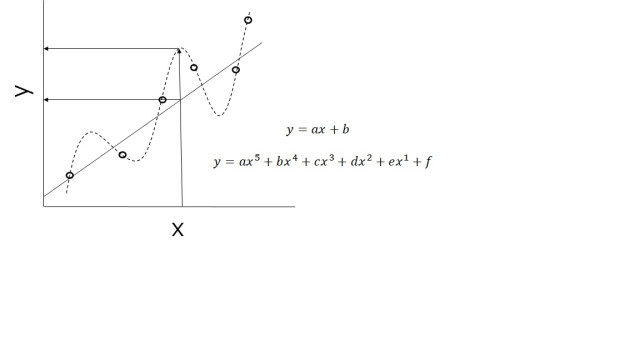
y = ax^5 + bx^4 + cx^3 + dx^2 + ex + f (2)
という別の数理モデルを使いたくなるかもしれません。
式(1)と式(2)、どちらを使うのが良いでしょうか?
(2)の場合、6個のパラメータ(a - f)を決めることができます(モデルを構築することができます)。しかも、この場合、すべてのデータポイントを通る曲線を描く(記述する)ことができます。すごいですね?!
しかし、この場合、構築したモデルを用いて、次のxからyを予測できるでしょうか?
図1を見ればわかる通り、予測に関しては、むしろ(1)の直線式を用いたほうがよさそうです。
パラメータ数を増やして数理モデルを複雑にすれば、既存データへのフィッテイングは必ず良くなります(相関係数は必ず良くなります)。
しかし、そのことで予測性が良くなるとは限りません。
数理モデルをより複雑にして、モデル構築に用いたデータ(training set)に対するフィッテイング(記述性)を良くしても、かえって予測性が下がってしまう場合があります(というより、よくあります)。これは、過剰適合(過剰学習)と呼ばれています。
「記述」と「予測」は全く異なること、モデルの選択は「記述性」ではなく「予測性」に基づいて行うべきであることは、是非覚えておいてください。一般に、予測性の検証は、モデル構築に用いていない、独立したデータ(test set)を用います。
過剰学習を防ぐには、フィッテイングの良さとパラメータ数のバランスを考える必要があります。一般には、観察結果を再現できる範囲で、なるべくパラメータ数を少なくするようにします。数学的には、赤池情報量基準(AIC)を計算します。AICの考え方は、古くから科学を導く指針とされてきた「オッカムの剃刀」と同じです。AICについては、各自お調べいただければと思います。数学的に、AICによるモデル選択は、データ数が多い場合、leave-one-out法による結果と同じになるのだそうです。
(非常に多くのPBPK論文で、フィッテイングに用いた臨床データに対するモデルによる記述が「予測(prediction)」として記載されています。臨床データに対してパラメータを当てはめているのですから、うまくあてはまって当たり前で、それを「予測」と言うのは間違いです。無知ゆえにそのように記載してしまっているのであれば研究者として勉強不足としか言いようがないですし、意図的に行っているのであればそれは捏造です。)
あと、もう一点、検量線で大切なことは、検量線が成立するのは、検量線の作成に用いたデータの範囲(内挿)に限られるということです。すなわち、観察データからパラメータを逆算した場合、その適応範囲は、内挿(interpolation)に限られます。
(C)薬物速度論の場合
以上のことは、薬物速度論とはどんな関係があるのでしょうか?
例えば、静脈内投与後の血中濃度推移(Cp(t))として、図2Aのようなデータが得られたとします。
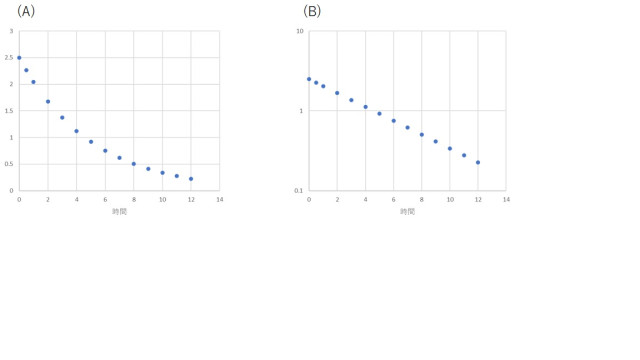
この時、縦軸の対数を採ると、図2Bのような直線関係が得られます。
したがって、このデータからは、2つのパラメータ(傾きと切片)を決定することができます。
1次反応速度を仮定すると、
Cp(t) = A exp (-a x t) (1コンパートメントモデル)
対数を採ると
ln Cp(t) = -a x t + ln A (y = ax + bと同じ形の数式)
したがって、傾きがa、切片がlnAになります。
もし、投与量(Dose)が分かっていれば(通常、分かっています)、Aから分布容積Vdを算出できます。
A = Dose/Vd
aは一般には、消失速度定数(kel)と呼ばれます。Vdが求まれば、kel = CL/Vdの関係から、CLを決定できます。
同様に、図3Aのようなデータの場合、縦軸の対数を採ると、2つの直線が現れます。したがって、この場合、4つのパラメータを決定することができます。
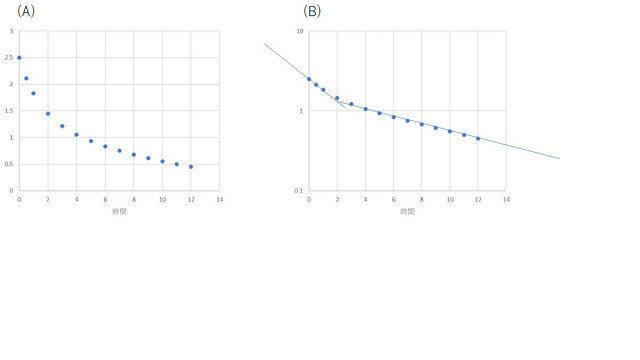
Cp(t) = A exp (-a x t) + B exp (-b x t) (2コンパートメントモデル)
さらにパラメータ数を増やせば、フィッテイングは良くなりますが、過剰適合に陥ってしまうかもしれません。
それでは、どのようにして数理モデルを選べばよいのでしょうか?グラフの見た目から何となく選んでも良いのですが、より数学的には、赤池情報量基準(AIC)を計算します。
なお、経口投与後の血中濃度推移の場合、通常3つのパラメータを同定できます。
Cp(t) = A ka/(ka-kel) (exp (-kel x t) - exp (-ka x t))
A = Dose x F/Vd
Fは、バイオアベイラビリティーです。
経口投与後の血中濃度推移データだけでは、VdとFを分離して個々に決定することはできません。VdとFを求めるには、別途、静脈内投与後の血中濃度推移が必要です。
さて、それでは、パラメータ数が数十から数百もある非常に複雑なPBPKモデルのパラメータを、血中濃度推移データから同定できるでしょうか?また、同定できたとして、構築されたモデルの「予測性」はどうなるでしょうか?
これは、次回のブログで説明したいと思います。
非常に複雑なPBPKモデルについてMiddle-out approachを考えるのは難しいので、簡単なモデル式を使って考えていきたいと思います。
(A)まずは、中学校数学の復習から。。。
中学校の時に、連立1次方程式について習いましたよね?
y = ax + b
という方程式のaとbを求めるにはどうすればよいか?という問題です。
ここでは、この式を、xという条件で実験をすると、yという値が得られる、という数理モデルとして考えます。
この場合、aとbを求めるには、xとyの組が、2つ必要です。
例えば
x = 1, y = 3
x = 2, y = 5
という実験データが得られた場合、
3 = a + b
5 = 2a + b
なので、上の式から、下の式を引いて、
-2 = -a
つまり
a = 2
です。これを上の式に代入すると、
3 = 2 + b
なのでb = 1。
しかがって、
y = 2x + 1
という式が得られました。
実際に、データを入れて試してみると
x = 1の時、y = 2x1 + 1 = 3
x = 2の時、y = 2x2 + 1 = 5
になりました。めでたし、めでたし。。。
(後述しますが、このことからわかるのは、実験結果に合うようにパラメータを逆算した場合(調整、最適化などとも言われますが)、逆算(=モデル構築)に用いた実験条件とその結果の関係をドンピシャで記述できるということです。このことと、異なる実験条件xから未知の実験結果yを「予測」できるかは、まったく別問題です。当たり前のことに思われるかもしれませんが、実際にはかなり混同されています。)
では、もし実験データが1組しかなかったら、どうなるでしょう?
モデル式y = ax + bに対して、実験データが
x = 1, y = 3
だけの場合を考えると、
3 = a + b
になります。
この数式を満たすaとbの組み合わせは、無限にあります。(a, b)= (0, 3), (1,2), (-1, 4)などなど
したがって、データが1組では、aとbを同定することはできません。(Un-identifiable)
同様に、
z = ax + by +c
の場合には、a,b,cを決めるには3つ以上の実験データの組が必要であり、
w = ax + by + cz + d
の場合には、a,b,c,dを決めるには4つ以上の実験データの組が必要です。
つまり、最低限パラメータ数だけ、実験データの組が必要です。
これは、どんなに高度なスーパーコンピュータを使っても、どんなアルゴリズムを使っても、絶対に回避することはできません。
(B) 検量線の話
さてところで、実際の研究では、
y = ax + b (1)
のaとbを、たった2組の(x,y)のデータポイントだけで決定することはありません。
例えば、検量線を作成する場合、少なくとも4-5点のデータポイントを採るでしょう。
ここで、仮に6つの実験データがある場合(図1)、

y = ax^5 + bx^4 + cx^3 + dx^2 + ex + f (2)
という別の数理モデルを使いたくなるかもしれません。
式(1)と式(2)、どちらを使うのが良いでしょうか?
(2)の場合、6個のパラメータ(a - f)を決めることができます(モデルを構築することができます)。しかも、この場合、すべてのデータポイントを通る曲線を描く(記述する)ことができます。すごいですね?!
しかし、この場合、構築したモデルを用いて、次のxからyを予測できるでしょうか?
図1を見ればわかる通り、予測に関しては、むしろ(1)の直線式を用いたほうがよさそうです。
パラメータ数を増やして数理モデルを複雑にすれば、既存データへのフィッテイングは必ず良くなります(相関係数は必ず良くなります)。
しかし、そのことで予測性が良くなるとは限りません。
数理モデルをより複雑にして、モデル構築に用いたデータ(training set)に対するフィッテイング(記述性)を良くしても、かえって予測性が下がってしまう場合があります(というより、よくあります)。これは、過剰適合(過剰学習)と呼ばれています。
「記述」と「予測」は全く異なること、モデルの選択は「記述性」ではなく「予測性」に基づいて行うべきであることは、是非覚えておいてください。一般に、予測性の検証は、モデル構築に用いていない、独立したデータ(test set)を用います。
過剰学習を防ぐには、フィッテイングの良さとパラメータ数のバランスを考える必要があります。一般には、観察結果を再現できる範囲で、なるべくパラメータ数を少なくするようにします。数学的には、赤池情報量基準(AIC)を計算します。AICの考え方は、古くから科学を導く指針とされてきた「オッカムの剃刀」と同じです。AICについては、各自お調べいただければと思います。数学的に、AICによるモデル選択は、データ数が多い場合、leave-one-out法による結果と同じになるのだそうです。
(非常に多くのPBPK論文で、フィッテイングに用いた臨床データに対するモデルによる記述が「予測(prediction)」として記載されています。臨床データに対してパラメータを当てはめているのですから、うまくあてはまって当たり前で、それを「予測」と言うのは間違いです。無知ゆえにそのように記載してしまっているのであれば研究者として勉強不足としか言いようがないですし、意図的に行っているのであればそれは捏造です。)
あと、もう一点、検量線で大切なことは、検量線が成立するのは、検量線の作成に用いたデータの範囲(内挿)に限られるということです。すなわち、観察データからパラメータを逆算した場合、その適応範囲は、内挿(interpolation)に限られます。
(C)薬物速度論の場合
以上のことは、薬物速度論とはどんな関係があるのでしょうか?
例えば、静脈内投与後の血中濃度推移(Cp(t))として、図2Aのようなデータが得られたとします。

この時、縦軸の対数を採ると、図2Bのような直線関係が得られます。
したがって、このデータからは、2つのパラメータ(傾きと切片)を決定することができます。
1次反応速度を仮定すると、
Cp(t) = A exp (-a x t) (1コンパートメントモデル)
対数を採ると
ln Cp(t) = -a x t + ln A (y = ax + bと同じ形の数式)
したがって、傾きがa、切片がlnAになります。
もし、投与量(Dose)が分かっていれば(通常、分かっています)、Aから分布容積Vdを算出できます。
A = Dose/Vd
aは一般には、消失速度定数(kel)と呼ばれます。Vdが求まれば、kel = CL/Vdの関係から、CLを決定できます。
同様に、図3Aのようなデータの場合、縦軸の対数を採ると、2つの直線が現れます。したがって、この場合、4つのパラメータを決定することができます。

Cp(t) = A exp (-a x t) + B exp (-b x t) (2コンパートメントモデル)
さらにパラメータ数を増やせば、フィッテイングは良くなりますが、過剰適合に陥ってしまうかもしれません。
それでは、どのようにして数理モデルを選べばよいのでしょうか?グラフの見た目から何となく選んでも良いのですが、より数学的には、赤池情報量基準(AIC)を計算します。
なお、経口投与後の血中濃度推移の場合、通常3つのパラメータを同定できます。
Cp(t) = A ka/(ka-kel) (exp (-kel x t) - exp (-ka x t))
A = Dose x F/Vd
Fは、バイオアベイラビリティーです。
経口投与後の血中濃度推移データだけでは、VdとFを分離して個々に決定することはできません。VdとFを求めるには、別途、静脈内投与後の血中濃度推移が必要です。
さて、それでは、パラメータ数が数十から数百もある非常に複雑なPBPKモデルのパラメータを、血中濃度推移データから同定できるでしょうか?また、同定できたとして、構築されたモデルの「予測性」はどうなるでしょうか?
これは、次回のブログで説明したいと思います。

